Karnaugh Map

Karnaugh Map

What is Karnaugh Map (K-maps)?

• ·        A graphical way to represent Boolean function.
• ·        A map is simply a table used to enumerate the values of a given Boolean expression for different input values.
• ·        Is a table with a cell for each minterm, which means it has a cell for each line of the truth table for the function.

Let’s s go through a few simple examples of K-maps.

Example 1

F(x,y)=xy

K-maps is shown below:

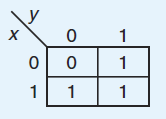
Example 2

F(x,y)=x+y

K-maps is shown below:

Explanation

Ø Three of the minterms in Example 2 have a value of 1, exactly the minterms for which the input to the function gives us a 1 for the output.

Ø To assign 1s in the K-map, we simply place 1s where we find corresponding 1s in the truth table.

Ø We can express the function F(x,y) = x + y as the logical OR of all minterms for which the minterm has a value of 1. know this function is simply x + y).

Ø We can minimize using Boolean identities:

Rules for K-map simplification

1.      The groups can only contain 1s; no 0s.

2.      Only 1s in adjacent cells can be grouped; diagonal grouping is not allowed.

3.      The number of 1s in a group must be a power of 2.

4.      The groups must be as large as possible while still following all rules.

5.      All 1s must belong to a group, even if it is a group of one.

6.      Overlapping groups are allowed.

7.      Wrap around is allowed.

8.      Use the fewest number of groups possible.

 ØGroups Contain Only 1s

      a) Incorrect                           b) Correct

Ø Groups Cannot Be Diagonal

      a) Incorrect                           b) Correct

Ø Groups Must Be Powers of 2

       a) Incorrect                           b) Correct

 Ø Groups Must Be as Large as Possible

        

             a) Incorrect                           b) Correct

K-map simplification for two variables

§  Please kindly refer the simple example above to know about this.

K-map simplification for three variables

You already know how to set up Kmaps for expressions involving two variables.

Let’s explore a few example for three variables.

§        Example 1

 ü  follow the rules for making groups.
ü  rules stipulate we must create thelargest groups whose sizes are powers of two.
ü  we group these as follows:

ü  Remember, we want to simplify the expression,

    and all we have to do is guarantee that every 1 is in some group.

ü  See how this parallels simplification using Boolean identities.

§  Example 2

ü  We have overlapping groups.

ü  We have a group that “wraps around.”

ü  The leftmost 1s in the first column can be grouped with the      rightmost 1s in the last column.

ü  The first and last rows of a Kmap are also logically adjacent.

ü  we group these as follows:

ü  final minimized function is 

K-map simplification for four variables

Let’s explore a example for three variables.

Minterms and Kmap Format for Four Variables

§  Example 1

ü  Group 1 is a “wrap-around” group.

ü  Group 2 represents the ultimate wrap-around group.

ü  Group 3 is easy to find.

ü  The final result is that F reduces to three terms, one from each group.

ü  The final reduction for F is then